Linear models data simulation¶
Generates Linear, Logistic and Poisson regression realizations given a weight vector.
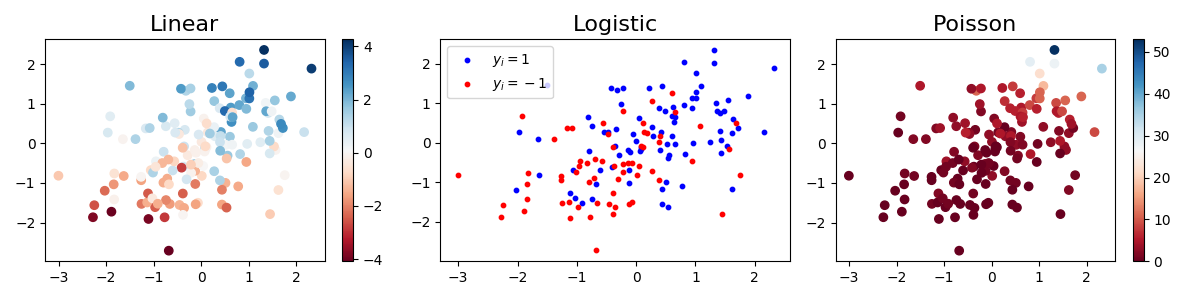
Python source code: plot_simulation_linear_model.py
import matplotlib.pyplot as plt
import numpy as np
from tick.linear_model import SimuLinReg, SimuLogReg, SimuPoisReg
n_samples, n_features = 150, 2
weights0 = np.array([0.3, 1.2])
intercept0 = 0.5
simu_linreg = SimuLinReg(weights0, intercept0, n_samples=n_samples, seed=123,
verbose=False)
X_linreg, y_linreg = simu_linreg.simulate()
simu_logreg = SimuLogReg(weights0, intercept0, n_samples=n_samples, seed=123,
verbose=False)
X_logreg, y_logreg = simu_logreg.simulate()
simu_poisreg = SimuPoisReg(weights0, intercept0, n_samples=n_samples,
link='exponential', seed=123, verbose=False)
X_poisreg, y_poisreg = simu_poisreg.simulate()
plt.figure(figsize=(12, 3))
plt.subplot(1, 3, 1)
plt.scatter(*X_linreg.T, c=y_linreg, cmap='RdBu')
plt.colorbar()
plt.title('Linear', fontsize=16)
plt.subplot(1, 3, 2)
plt.scatter(*X_logreg[y_logreg == 1].T, color='b', s=10, label=r'$y_i=1$')
plt.scatter(*X_logreg[y_logreg == -1].T, color='r', s=10, label=r'$y_i=-1$')
plt.legend(loc='upper left')
plt.title('Logistic', fontsize=16)
plt.subplot(1, 3, 3)
plt.scatter(*X_poisreg.T, c=y_poisreg, cmap='RdBu')
plt.colorbar()
plt.title('Poisson', fontsize=16)
plt.tight_layout()
plt.show()
Total running time of the example: 0.25 seconds ( 0 minutes 0.25 seconds)
- Mentioned tick classes: