tick.robust

This module provides tools for robust inference of generalized linear models and outliers detection. It proposes two set of things: a learner for least-squares regression with individual intercepts, see 1. Regression with individual intercepts and a set of losses for robust supervised learning, see 2. Robust losses.

1. Regression with individual intercepts

In this section, we describe the approach used in the RobustLinearRegression learner. It allows to detect outliers and to fit a least-squares regression model at the same time. Namely, given training data \((x_i, y_i) \in \mathbb R^d \times \mathbb R\) for \(i=1, \ldots, n\), it considers the following problem

\[\frac 1n \sum_{i=1}^n \ell(y_i, x_i^\top w + b + \mu_i) + s \sum_{j=1}^{d} c_j | w_{(j)} | + g(w),\]

where \(|w_{(j)}|\) is decreasing, \(w \in \mathbb R^d\) is a vector containing the model weights, \(\mu = [\mu_1 \cdots \mu_n] \in \mathbb R^n\) is a vector containing individual intercepts, \(b \in \mathbb R\) is the population intercept, \(\ell : \mathbb R^2 \rightarrow \mathbb R\) is the least-squares loss and \(g\) is a penalization function for the model weights, for which different choices are possible, see tick.prox. Note that in this problem the vector of individual intercepts \(\mu\) is penalized by a sorted-L1 norm, also called SLOPE, see tick.prox for details, where the weights are given by

\[w_j = \Phi \Big( 1 - \frac{j \alpha}{2 n} \Big),\]

where \(\alpha\) stands for the FDR level for the support detection of \(\mu\), that can be tuned with the fdr parameter. The global penalization level \(s\) corresponds to the inverse of the C_sample_intercepts parameter.

RobustLinearRegression(C_sample_intercepts)

Robust linear regression learner.

Tools for robust estimation of the standard-deviation

Some tools for the robust estimation of the standard deviation are also provided.

std_mad(x)

Robust estimation of the standard deviation, based on the Corrected Median Absolute Deviation (MAD) of x.

std_iqr(x)

Robust estimation of the standard deviation, based on the inter-quartile (IQR) distance of x.

Example

"""
===========================
Robust linear model example
===========================

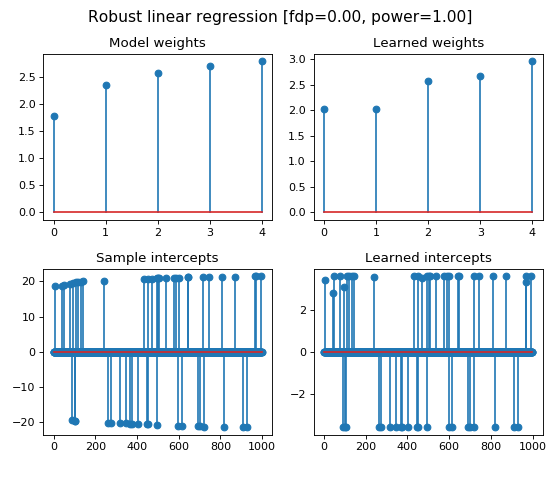
In this example with simulate a linear regression model with 1000 samples and
5 features. The simulated data is contaminated by 20% of outliers, in the form
of sparse sample intercepts (thus only on 20% of samples).

We illustrate the estimated linear regression weights and sample intercepts
obtained by the ``RobustLinearRegression`` learner, where we also compute the
false discovery proportion and power of the method for the multi-test problem of
outliers detection.
Note that the penalization level ``C_sample_intercepts`` of the sample
intercepts should be chosen as n_samples / noise_level, where noise_level is
obtained by a robust estimation of the noise's standard deviation.
We simply use here the `tick.inference.std_iqr` estimator.

Note that we don't use penalization on the model weights here, while other
penalizations are available, by changing the ``penalty`` parameter and by
giving a ``C`` value for the level of penalization.
Default is ``penalty='l2'``, namely ridge penalization, while ``penalty='l1'``
or ``penalty='slope'`` can be used when the number of features is large.
"""
import numpy as np
from matplotlib import pyplot as plt
from tick.simulation import weights_sparse_gauss, \
    features_normal_cov_toeplitz
from tick.robust import RobustLinearRegression, std_iqr
from tick.metrics import support_fdp, support_recall

np.random.seed(1)

n_samples = 1000
n_features = 5
noise_level = 1.
n_outliers = 50
outliers_intensity = 5.

intercept0 = -3.
log_linspace = np.log(n_features * np.linspace(1, 10, n_features))
weights0 = np.sqrt(2 * log_linspace)

sample_intercepts0 = weights_sparse_gauss(n_weights=n_samples, nnz=n_outliers)
idx_nnz = sample_intercepts0 != 0
log_linspace = np.log(n_samples * np.linspace(1, 10, n_outliers))
sample_intercepts0[idx_nnz] = outliers_intensity * np.sqrt(2 * log_linspace) \
    * np.sign(sample_intercepts0[idx_nnz])

X = features_normal_cov_toeplitz(n_samples, n_features, 0.5)

y = X.dot(weights0) + noise_level * np.random.randn(n_samples) \
    + intercept0 + sample_intercepts0

target_fdr = 0.1
noise_level = std_iqr(y)
learner = RobustLinearRegression(
    C_sample_intercepts=2 * n_samples / noise_level, penalty='none',
    fdr=target_fdr, verbose=False)
learner.fit(X, y)

fdp_ = support_fdp(sample_intercepts0, learner.sample_intercepts)
power_ = support_recall(sample_intercepts0, learner.sample_intercepts)

fig = plt.figure(figsize=(7, 6))
titles = [
    'Model weights', 'Learned weights', 'Sample intercepts',
    'Learned intercepts'
]
vectors = [
    weights0, learner.weights, sample_intercepts0, learner.sample_intercepts
]
for idx_plot, title, vector in zip(range(221, 225), titles, vectors):
    ax = fig.add_subplot(idx_plot)
    ax.stem(vector)
    ax.set_title(title, fontsize=12)
fig.suptitle(
    'Robust linear regression [fdp=%.2f, power=%.2f]' % (fdp_, power_),
    fontsize=14)
fig.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

(Source code, png, hires.png, pdf)

../_images/plot_robust_linear_regression2.png

2. Robust losses

Tick also provides losses for robust inference when it is believed that data contains outliers. It also provides the model ModelLinRegWithIntercepts which is used in the RobustLinearRegression described above.

Model

Type

Label type

Class

Linear regression with intercepts

Regression

Continuous

ModelLinRegWithIntercepts

Huber regression

Regression

Continuous

ModelHuber

Epsilon-insensitive regression

Regression

Continuous

ModelEpsilonInsensitive

Absolute regression

Regression

Continuous

ModelAbsoluteRegression

Modified Huber loss

Classification

Binary

ModelModifiedHuber

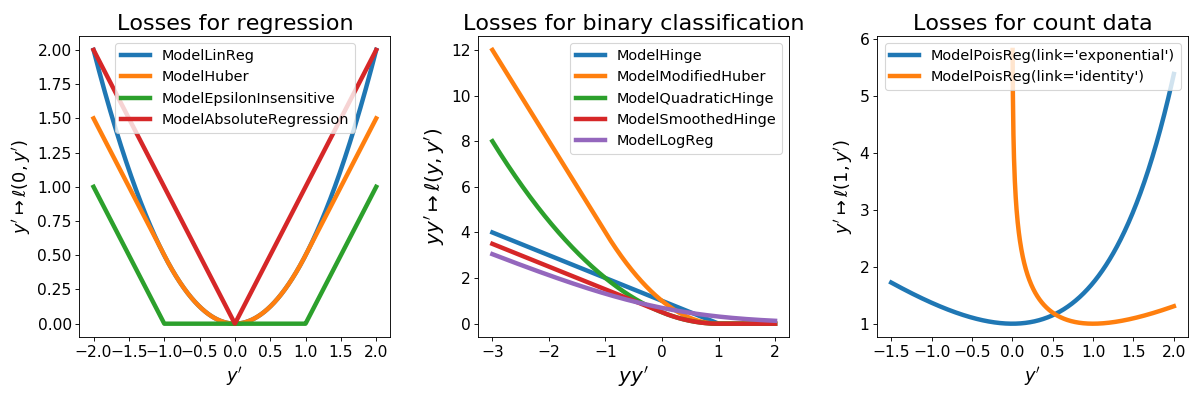
The robust losses are illustrated in the following picture, among the other losses provided in the tick.linear_model module.

(Source code, png, hires.png, pdf)

../_images/plot_linear_model_losses1.png

ModelHuber

The Huber loss for robust regression (less sensitive to outliers) is given by

\[\begin{split}\ell(y, y') = \begin{cases} \frac 12 (y' - y)^2 &\text{ if } |y' - y| \leq \delta \\ \delta (|y' - y| - \frac 12 \delta) &\text{ if } |y' - y| > \delta \end{cases}\end{split}\]

for \(y, y' \in \mathbb R\), where \(\delta > 0\) can be tuned using the threshold argument.

ModelEpsilonInsensitive

Epsilon-insensitive loss, given by

\[\begin{split}\ell(y, y') = \begin{cases} |y' - y| - \epsilon &\text{ if } |y' - y| > \epsilon \\ 0 &\text{ if } |y' - y| \leq \epsilon \end{cases}\end{split}\]

for \(y, y' \in \mathbb R\), where \(\epsilon > 0\) can be tuned using the threshold argument.

ModelAbsoluteRegression

The L1 loss given by

\[\ell(y, y') = |y' - y|\]

for \(y, y' \in \mathbb R\)

ModelModifiedHuber

The modified Huber loss, used for robust classification (less sensitive to outliers). The loss is given by

\[\begin{split}\ell(y, y') = \begin{cases} - 4 y y' &\text{ if } y y' \leq -1 \\ (1 - y y')^2 &\text{ if } -1 < y y' < 1 \\ 0 &\text{ if } y y' \geq 1 \end{cases}\end{split}\]

for \(y \in \{ -1, 1\}\) and \(y' \in \mathbb R\)