tick.survival¶

"""
==============================
Cox regression data simulation
==============================

Generates Cox Regression realization given a weight vector 
"""

import matplotlib.pyplot as plt
import numpy as np
from tick.survival import SimuCoxReg

n_samples = 150
weights = np.array([0.3, 1.2])

seed = 123
simu_coxreg = SimuCoxReg(weights, n_samples=n_samples, seed=123, verbose=False)
X, T, C = simu_coxreg.simulate()

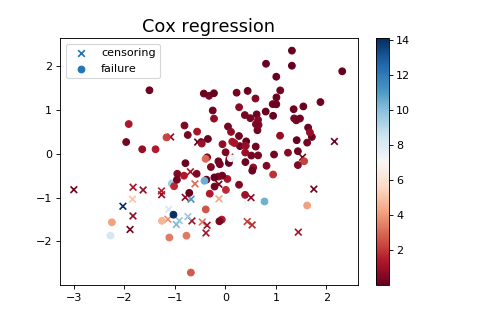
plt.figure(figsize=(6, 4))

plt.scatter(*X[C == 0].T, c=T[C == 0], cmap='RdBu', marker="x",
            label="censoring")
plt.scatter(*X[C == 1].T, c=T[C == 1], cmap='RdBu', marker="o",
            label="failure")
plt.colorbar()
plt.legend(loc='upper left')
plt.title('Cox regression', fontsize=16)

"""
====================================================================
ConvSCCS cross validation on simulated longitudinal features example
====================================================================

In this example we simulate longitudinal data with preset relative incidence
for each feature. We then perform a cross validation of the ConvSCCS model
and compare the estimated coefficients to the relative incidences used for
the simulation.
"""
from time import time
import numpy as np
from scipy.sparse import csr_matrix, hstack
from matplotlib import cm
import matplotlib.pylab as plt
from tick.survival.simu_sccs import CustomEffects
from tick.survival import SimuSCCS, ConvSCCS
from mpl_toolkits.axes_grid1 import make_axes_locatable

# Simulation parameters
seed = 0
lags = 49
n_samples = 2000
n_intervals = 750
n_corr = 3

# Relative incidence functions used for the simulation
ce = CustomEffects(lags + 1)
null_effect = [ce.constant_effect(1)] * 2
intermediate_effect = ce.bell_shaped_effect(2, 30, 15, 15)
late_effects = ce.increasing_effect(2, curvature_type=4)

sim_effects = [*null_effect, intermediate_effect, late_effects]

n_features = len(sim_effects)
n_lags = np.repeat(lags, n_features).astype('uint64')

coeffs = [np.log(c) for c in sim_effects]

# Time drift (age effect) used for the simulations.
time_drift = lambda t: np.log(8 * np.sin(.01 * t) + 9)

# Simaltion of the features.
sim = SimuSCCS(n_samples, n_intervals, n_features, n_lags,
               time_drift=time_drift, coeffs=coeffs, seed=seed,
               n_correlations=n_corr, verbose=False)
features, censored_features, labels, censoring, coeffs = sim.simulate()

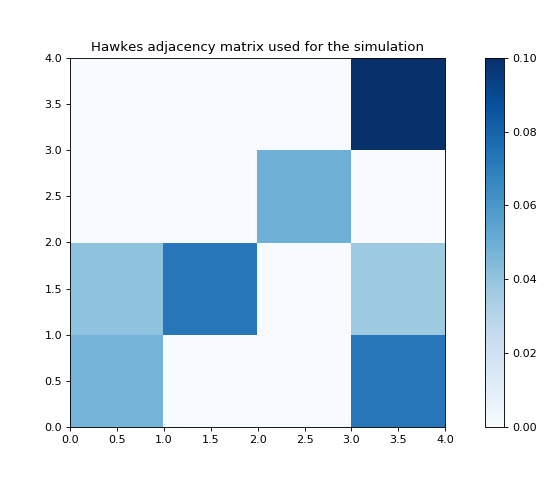
# Plot the Hawkes kernel matrix used to generate the features.
fig, ax = plt.subplots(figsize=(7, 6))
heatmap = ax.pcolor(sim.hawkes_exp_kernels.adjacency, cmap=cm.Blues)
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.5)
fig.colorbar(heatmap, cax=cax)
ax.set_title('Hawkes adjacency matrix used for the simulation')
plt.show()

## Add age_groups features to feature matrices.
agegrps = [0, 125, 250, 375, 500, 625, 750]
n_agegrps = len(agegrps) - 1

feat_agegrp = np.zeros((n_intervals, n_agegrps))
for i in range(n_agegrps):
    feat_agegrp[agegrps[i]:agegrps[i + 1], i] = 1

feat_agegrp = csr_matrix(feat_agegrp)
features = [hstack([f, feat_agegrp]).tocsr() for f in features]
censored_features = [
    hstack([f, feat_agegrp]).tocsr() for f in censored_features
]
n_lags = np.hstack([n_lags, np.zeros(n_agegrps)])

# Learning
# Example code for cross validation
# start = time()
# learner = ConvSCCS(n_lags=n_lags.astype('uint64'),
#                    penalized_features=np.arange(n_features),
#                    random_state=42)
# C_TV_range = (1, 4)
# C_L1_range = (2, 5)
# _, cv_track = learner.fit_kfold_cv(features, labels, censoring,
#                                    C_TV_range, C_L1_range,
#                                    confidence_intervals=True,
#                                    n_samples_bootstrap=20, n_cv_iter=50)
# elapsed_time = time() - start
# print("Elapsed time (model training): %.2f seconds \n" % elapsed_time)
# print("Best model hyper parameters: \n")
# print("C_tv : %f \n" % cv_track.best_model['C_tv'])
# print("C_group_l1 : %f \n" % cv_track.best_model['C_group_l1'])
# cv_track.plot_cv_report(35, 45)
# plt.show()
# confidence_intervals = cv_track.best_model['confidence_intervals']

# using the parameters resulting from cross-validation
learner = ConvSCCS(
    n_lags=n_lags.astype('uint64'), penalized_features=np.arange(n_features),
    random_state=42, C_tv=270.2722840570933, C_group_l1=5216.472772625124)

_, confidence_intervals = learner.fit(features, labels, censoring,
                                      confidence_intervals=True,
                                      n_samples_bootstrap=20)

# Plot estimated parameters
# get bootstrap confidence intervals
refitted_coeffs = confidence_intervals['refit_coeffs']
lower_bound = confidence_intervals['lower_bound']
upper_bound = confidence_intervals['upper_bound']

n_rows = int(np.ceil(n_features / 2))
remove_last_plot = (n_features % 2 != 0)

fig, axarr = plt.subplots(n_rows, 2, sharex=True, sharey=True, figsize=(10, 6))
y = confidence_intervals['refit_coeffs']
lb = confidence_intervals['lower_bound']
ub = confidence_intervals['upper_bound']
for i, c in enumerate(y[:-6]):
    ax = axarr[i // 2][i % 2]
    l = n_lags[i]
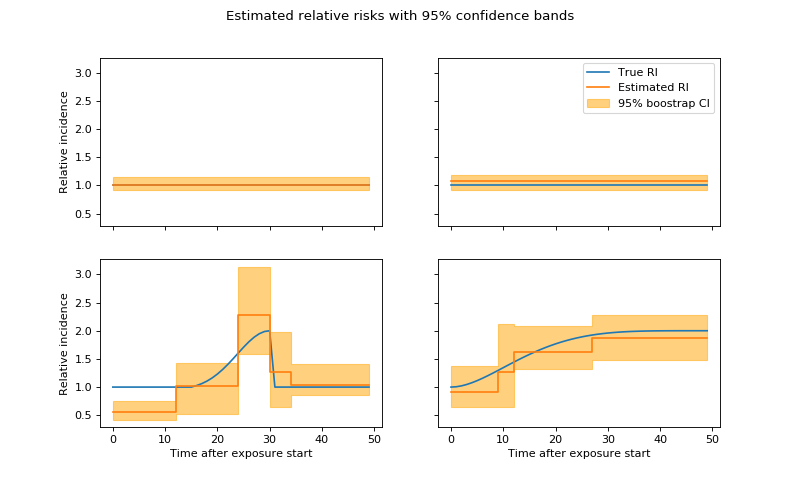
    ax.plot(np.exp(coeffs[i]), label="True RI")
    ax.step(np.arange(l + 1), np.exp(c), label="Estimated RI")
    ax.fill_between(
        np.arange(l + 1), np.exp(lb[i]), np.exp(ub[i]), alpha=.5,
        color='orange', step='pre', label="95% boostrap CI")
plt.suptitle('Estimated relative risks with 95% confidence bands')
axarr[0][1].legend(loc='best')
[ax[0].set_ylabel('Relative incidence') for ax in axarr]
[ax.set_xlabel('Time after exposure start') for ax in axarr[-1]]
if remove_last_plot:
    fig.delaxes(axarr[-1][-1])
plt.show()

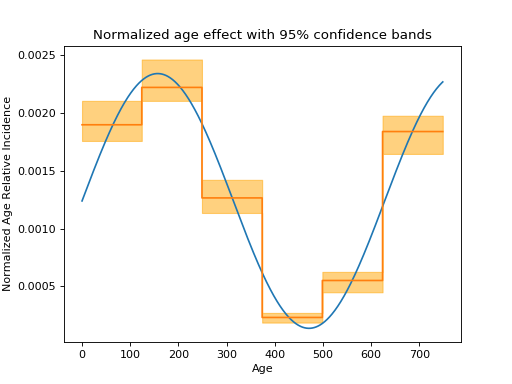
normalize = lambda x: x / np.sum(x)
m = np.repeat(np.hstack(refitted_coeffs[-6:]), 125)
lb = np.repeat(np.hstack(lower_bound[-6:]), 125)
ub = np.repeat(np.hstack(upper_bound[-6:]), 125)
plt.figure()
plt.plot(
    np.arange(n_intervals),
    normalize(np.exp(time_drift(np.arange(n_intervals)))))
plt.step(np.arange(n_intervals), normalize(np.exp(m)))
plt.fill_between(
    np.arange(n_intervals),
    np.exp(lb) / np.exp(m).sum(),
    np.exp(ub) / np.exp(m).sum(), alpha=.5, color='orange', step='pre')
plt.xlabel('Age')
plt.ylabel('Normalized Age Relative Incidence')
plt.title("Normalized age effect with 95% confidence bands")
plt.show()