tick.solver

This is a solver toolbox, which is used to train almost all models in tick. It features two types of solvers: deterministic and stochastic. Deterministic solvers use a full pass over data at each iteration, while stochastic solvers make epoch_size iterations within each iteration. Most of the optimization problems considered here can be written as

\[\min_w f(w) + g(w)\]

where \(f\) is a goodness-of-fit term, which depends on the model considered, and \(g\) is a function penalizing \(w\) (see the tick.prox module).

1. The solver class API

All the solvers have a set_model method, which corresponds to the function \(f\) to pass the model to be trained, and a set_prox method to pass the penalization, which corresponds to the \(g\). The solver is launched using the solve method to which a starting point and eventually a step-size can be given. Here is an example, another example is also given below.

import numpy as np
from tick.linear_model import SimuLogReg, ModelLogReg
from tick.simulation import weights_sparse_gauss
from tick.solver import SVRG
from tick.prox import ProxElasticNet

n_samples, n_features = 5000, 10
weights0 = weights_sparse_gauss(n_weights=n_features, nnz=3)
intercept0 = 1.
X, y = SimuLogReg(weights0, intercept=intercept0, seed=123,
                  n_samples=n_samples, verbose=False).simulate()

model = ModelLogReg(fit_intercept=True).fit(X, y)
prox = ProxElasticNet(strength=1e-3, ratio=0.5, range=(0, n_features))

svrg = SVRG(tol=0., max_iter=5, print_every=1).set_model(model).set_prox(prox)
x0 = np.zeros(model.n_coeffs)
minimizer = svrg.solve(x0, step=1 / model.get_lip_max())
print("\nfound minimizer\n", minimizer)

which outputs

Launching the solver SVRG...
  n_iter  |    obj    |  rel_obj
        1 |  5.01e-01 |  5.15e-02
        2 |  4.97e-01 |  8.44e-03
        3 |  4.97e-01 |  5.00e-04
        4 |  4.97e-01 |  2.82e-05
        5 |  4.97e-01 |  7.28e-07

Done solving using SVRG in 0.03281998634338379 seconds

found minimizer
 [ 0.01992683  0.00456966 -0.16595686 -0.08619878  0.01059461  0.6144692
  0.0049031  -0.07767023  0.07550217  1.18493663  0.9424508 ]

Note the argument step=1 / model.get_lip_max()) passed to the solve method that gives an automatic tuning of the step size.

2. Available solvers

Here is the list of the solvers available in tick. Note that a lot of details about each solver is available in the classes documentations, linked below.

Solver

Class

Proximal gradient descent

GD

Accelerated proximal gradient descent

AGD

Broyden, Fletcher, Goldfarb, and Shannon (quasi-newton)

BFGS

Self-Concordant Proximal Gradient Descent

SCPG

Generalized Forward-Backward

GFB

Stochastic Gradient Descent

SGD

Adaptive Gradient Descent solver

AdaGrad

Stochastic Variance Reduced Descent

SVRG

Stochastic Averaged Gradient Descent

SAGA

Stochastic Dual Coordinate Ascent

SDCA

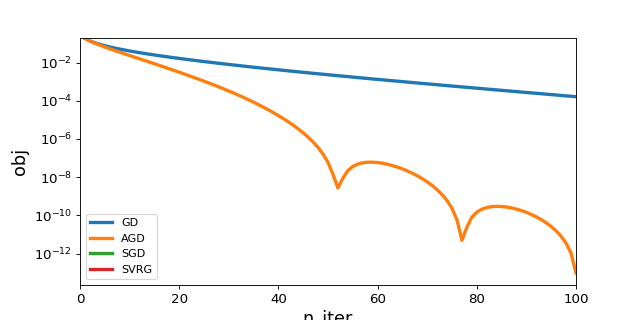
3. Example

Here is an example of combination of a model a prox and a solver to compare the training time of several solvers for logistic regression with the elastic-net penalization. Note that, we specify a range=(0, n_features) so that the intercept is not penalized (see tick.prox for more details).

import numpy as np
from tick.linear_model import ModelLogReg ,SimuLogReg
from tick.simulation import weights_sparse_gauss
from tick.solver import GD, AGD, SGD, SVRG, SDCA
from tick.prox import ProxElasticNet, ProxL1
from tick.plot import plot_history

n_samples, n_features, = 5000, 50
weights0 = weights_sparse_gauss(n_features, nnz=10)
intercept0 = 0.2
X, y = SimuLogReg(weights=weights0, intercept=intercept0,
                  n_samples=n_samples, seed=123, verbose=False).simulate()

model = ModelLogReg(fit_intercept=True).fit(X, y)
prox = ProxElasticNet(strength=1e-3, ratio=0.5, range=(0, n_features))

solver_params = {'max_iter': 100, 'tol': 0., 'verbose': False}
x0 = np.zeros(model.n_coeffs)

gd = GD(linesearch=False, **solver_params).set_model(model).set_prox(prox)
gd.solve(x0, step=1 / model.get_lip_best())

agd = AGD(linesearch=False, **solver_params).set_model(model).set_prox(prox)
agd.solve(x0, step=1 / model.get_lip_best())

sgd = SGD(**solver_params).set_model(model).set_prox(prox)
sgd.solve(x0, step=500.)

svrg = SVRG(**solver_params).set_model(model).set_prox(prox)
svrg.solve(x0, step=1 / model.get_lip_max())

plot_history([gd, agd, sgd, svrg], log_scale=True, dist_min=True)

(Source code, png, hires.png, pdf)

../_images/plot_solver_comparison1.png