tick.prox

This module proposes a large number of proximal operator, allowing the use many penalization techniques for model fitting. Namely, most optimization problems considered in tick (but not all) can be written as

\[\min_w f(w) + g(w)\]

where \(f\) is a goodness-of-fit term and \(g\) is a function penalizing \(w\). Depending on the problem, you might want to use some function \(g\) in order to induce a specific property of the weights \(w\) of the model.

The proximal operator of a convex function \(g\) at some point \(w\) is defined as the unique minimizer of the problem

\[\text{prox}_{g}(w, t) = \text{argmin}_{w'} \Big\{ \frac 12 \| w - w' \|_2^2 + t g(w') \Big\}\]

where \(t > 0\) is a regularization parameter and \(\| \cdot \|_2\) is the Euclidean norm. Note that in the particular case where \(g(w) = \delta_{C}(w)\), with \(C\) a convex set, then \(\text{prox}_g\) is a projection operator (here \(\delta_{C}(w) = 0\) if \(w \in C\) and \(+\infty\) otherwise).

Depending on the problem, \(g\) might actually be used only a subset of entries of \(w\). For instance, in a generalized linear models, \(w\) corresponds to the concatenation of model weights and intercept, and the latter should not be penalized, see tick.linear_model. To solve this issue, in all prox classes, an optional range parameter is available, to apply the regularization only to a subset of entries of \(w\).

1. Available operators

The list of available operators in tick given in the next table.

Penalization

Function

Class

Identity

\(g(w) = 0\)

ProxZero

L1 norm

\(g(w) = s \sum_{j=1}^d |w_j|\)

ProxL1

L1 norm with weights

\(g(w) = s \sum_{j=1}^d c_j |w_j|\)

ProxL1w

Ridge

\(g(w) = s \sum_{j=1}^d \frac{w_j^2}{2}\)

ProxL2Sq

L2 norm

\(g(w) = s \sqrt{d \sum_{j=1}^d w_j^2}\)

ProxL2

Elastic-net

\(g(w) = s \Big(\sum_{j=1}^{d} \alpha |w_j| + (1 - \alpha) \frac{w_j^2}{2} \Big)\)

ProxElasticNet

Nuclear norm

\(g(w) = s \sum_{j=1}^{q} \sigma_j(w)\)

ProxNuclear

Non-negative constraint

\(g(w) = s \delta_C(w)\) where \(C=\) set of vectors with non-negative entries

ProxPositive

Equality constraint

\(g(w) = s \delta_C(w)\) where \(C=\) set of vectors with identical entries

ProxEquality

Sorted L1

\(g(w) = s \sum_{j=1}^{d} c_j |w_{(j)}|\) where \(|w_{(j)}|\) is decreasing

ProxSlope

Total-variation

\(g(w) = s \sum_{j=2}^d |w_j - w_{j-1}|\)

ProxTV

Binarsity

\(g(w) = s \sum_{j=1}^d \big( \sum_{k=2}^{d_j} |w_{j,k} - w_{j,k-1} | + \delta_C(w_{j,\bullet}) \big)\)

ProxBinarsity

Group L1

\(g(w) = s \sum_{j=1}^d \sqrt{d_j} \| w^{(j)}\|_2\)

ProxGroupL1

2. Example

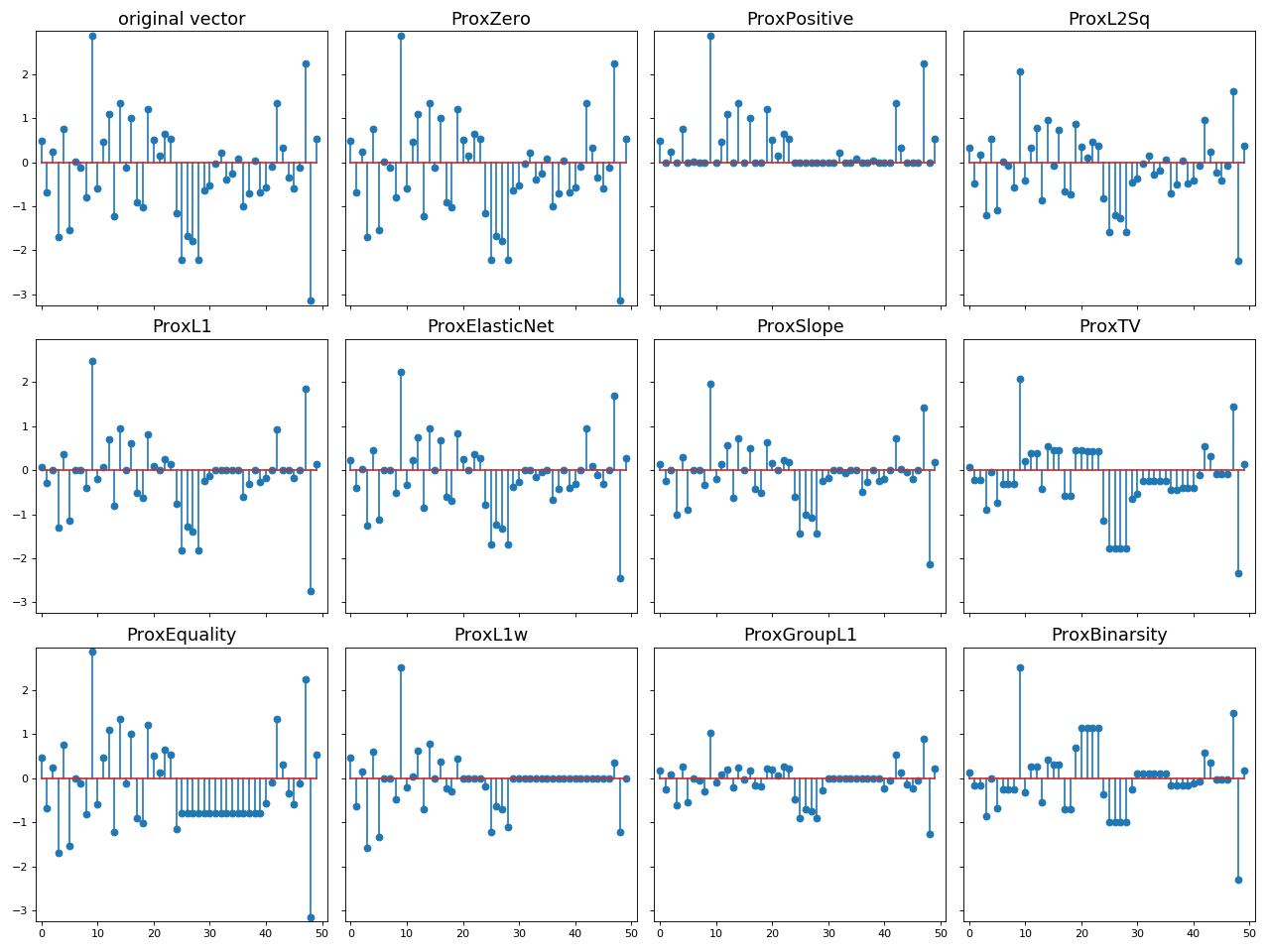
Here is an illustration of the effect of these proximal operators on an example.

"""
==============================
Examples of proximal operators
==============================

Plot examples of proximal operators available in tick
"""
import numpy as np
import matplotlib.pyplot as plt
from tick.prox import ProxL1, ProxElasticNet, ProxL2Sq, \
    ProxPositive, ProxSlope, ProxTV, ProxZero, ProxBinarsity, ProxGroupL1, \
    ProxEquality, ProxL1w

np.random.seed(12)
x = np.random.randn(50)
a, b = x.min() - 1e-1, x.max() + 1e-1
s = 0.4

proxs = [
    ProxZero(),
    ProxPositive(),
    ProxL2Sq(strength=s),
    ProxL1(strength=s),
    ProxElasticNet(strength=s, ratio=0.5),
    ProxSlope(strength=s),
    ProxTV(strength=s),
    ProxEquality(range=(25, 40)),
    ProxL1w(strength=s, weights=0.1 * np.arange(50, dtype=np.double)),
    ProxGroupL1(strength=2 * s, blocks_start=np.arange(0, 50, 10),
                blocks_length=10 * np.ones((5,))),
    ProxBinarsity(strength=s, blocks_start=np.arange(0, 50, 10),
                  blocks_length=10 * np.ones((5,)))
]

fig, _ = plt.subplots(3, 4, figsize=(16, 12), sharey=True, sharex=True)
fig.axes[0].stem(x)
fig.axes[0].set_title("original vector", fontsize=16)
fig.axes[0].set_xlim((-1, 51))
fig.axes[0].set_ylim((a, b))

for i, prox in enumerate(proxs):
    fig.axes[i + 1].stem(prox.call(x))
    fig.axes[i + 1].set_title(prox.name, fontsize=16)
    fig.axes[i + 1].set_xlim((-1, 51))
    fig.axes[i + 1].set_ylim((a, b))

plt.tight_layout()
plt.show()

(Source code, png, hires.png, pdf)

../_images/plot_prox_example2.png

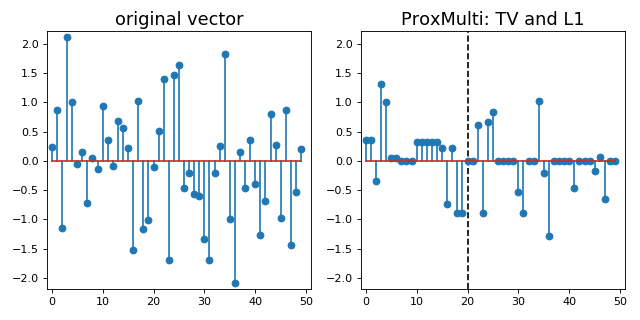
3. How to combine several prox ?

Another prox class is the ProxMulti that allows to combine any proximal operators together. It simply applies sequentially each operator passed to ProxMulti, one after the other. Here is an example of combination of a total-variation penalization and L1 penalization applied to different parts of a vector.

import numpy as np
import matplotlib.pyplot as plt
from tick.prox import ProxL1, ProxTV, ProxMulti

s = 0.4

prox = ProxMulti(
    proxs=(
        ProxTV(strength=s, range=(0, 20)),
        ProxL1(strength=2 * s, range=(20, 50))
    )
)

x = np.random.randn(50)
a, b = x.min() - 1e-1, x.max() + 1e-1

plt.figure(figsize=(8, 4))
plt.subplot(1, 2, 1)
plt.stem(x)
plt.title("original vector", fontsize=16)
plt.xlim((-1, 51))
plt.ylim((a, b))
plt.subplot(1, 2, 2)
plt.stem(prox.call(x))
plt.title("ProxMulti: TV and L1", fontsize=16)
plt.xlim((-1, 51))
plt.ylim((a, b))
plt.vlines(20, a, b, linestyles='dashed')
plt.tight_layout()
plt.show()

(Source code, png, hires.png, pdf)

../_images/plot_prox_multi1.png

4. The prox class API

Let us describe the prox API with the ProxL1 class, that provides the proximal operator of the function \(g(w) = s \|w\|_1 = s \sum_{j=1}^d |w_j|\), where \(s\) corresponds to the strength of penalization, and can be tuned using the strength parameter.

import numpy as np
from tick.prox import ProxL1

prox = ProxL1(strength=1e-2)
print(prox)

prints

{
  "dtype": "float64",
  "name": "ProxL1",
  "positive": false,
  "range": null,
  "strength": 0.01
}

The positive parameter allows to enforce positivity, namely when positive=True then the considered function is actually \(g(w) = s \|w\|_1 + \delta_{C}(x)\) where \(C\) is the set of vectors with non-negative entries. Note that no range was specified to this prox so that it is null (None) for now.

prox = ProxL1(strength=1e-2, range=(0, 30), positive=True)
print(prox)

prints

{
  "dtype": "float64",
  "name": "ProxL1",
  "positive": true,
  "range": [
    0,
    30
  ],
  "strength": 0.01
}

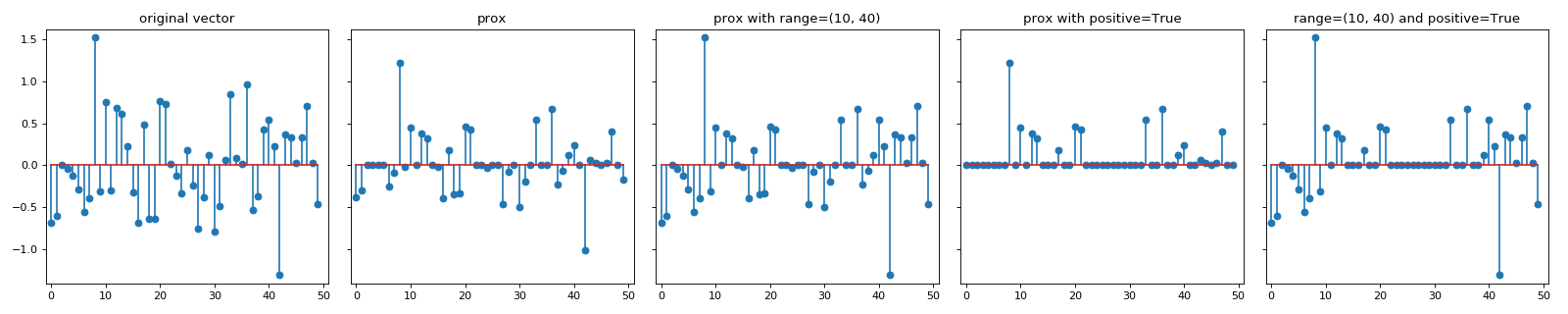
All prox classes provide a method call that computes \(\text{prox}_{g}(w, t)\) where \(t\) is a parameter passed using the step argument. The output of call can optionally be passed using the out argument (this allows to avoid unnecessary copies, and thus extra memory allocation).

import numpy as np
import matplotlib.pyplot as plt
from tick.prox import ProxL1

x = 0.5 * np.random.randn(50)
a, b = x.min() - 1e-1, x.max() + 1e-1

proxs = [
    ProxL1(strength=0.),
    ProxL1(strength=3e-1),
    ProxL1(strength=3e-1, range=(10, 40)),
    ProxL1(strength=3e-1, positive=True),
    ProxL1(strength=3e-1, range=(10, 40), positive=True),
]

names = [
    "original vector",
    "prox",
    "prox with range=(10, 40)",
    "prox with positive=True",
    "range=(10, 40) and positive=True",
]

_, ax_list = plt.subplots(1, 5, figsize=(20, 4), sharey=True)

for prox, name, ax in zip(proxs, names, ax_list):
    ax.stem(prox.call(x))
    ax.set_title(name)
    ax.set_xlim((-1, 51))
    ax.set_ylim((a, b))

plt.tight_layout()
plt.show()

(Source code, png, hires.png, pdf)

../_images/plot_prox_api1.png

The value of \(g\) is simply obtained using the value method

prox = ProxL1(strength=1., range=(5, 10))
val = prox.value(np.arange(10, dtype=np.double))
print(val)

simply prints

35.0

which corresponds to the sum of integers between 5 and 9 included.