tick.linear_model.ModelPoisReg¶
-
class
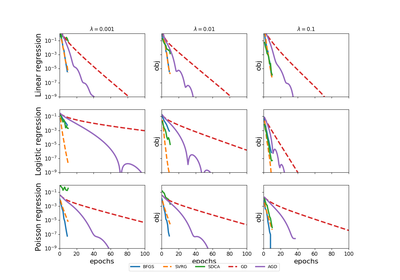
tick.linear_model.ModelPoisReg(fit_intercept: bool = True, link: str = 'exponential', n_threads: int = 1)[source]¶ Poisson regression model with identity or exponential link for data with a count label. This class gives first order and second order information for this model (gradient, loss and hessian norm) and can be passed to any solver through the solver’s
set_modelmethod. Can lead to overflows with some solvers (see the note below).Given training data \((x_i, y_i) \in \mathbb R^d \times \mathbb N\) for \(i=1, \ldots, n\), this model considers a goodness-of-fit
\[f(w, b) = \frac 1n \sum_{i=1}^n \ell(y_i, b + x_i^\top w),\]where \(w \in \mathbb R^d\) is a vector containing the model-weights, \(b \in \mathbb R\) is the intercept (used only whenever
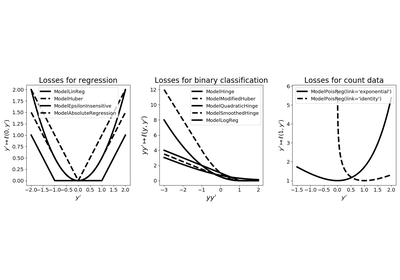
fit_intercept=True) and \(\ell : \mathbb R^2 \rightarrow \mathbb R\) is the loss given by\[\ell(y, y') = e^{y'} - y y'\]whenever
link='exponential'and\[\ell(y, y') = y' - y \log(y')\]whenever
link='identity', for \(y \in \mathbb N\) and \(y' \in \mathbb R\). Data is passed to this model through thefit(X, y)method where X is the features matrix (dense or sparse) and y is the vector of labels.- Parameters
fit_intercept :
boolIf
True, the model uses an interceptlink :
str, default=”exponential”Type of link function
if
"identity": the intensity is the inner product of the model’s coeffs with the features. In this case, one must ensure that the intensity is non-negativeif
"exponential": the intensity is the exponential of the inner product of the model’s coeffs with the features.
Note that link cannot be changed after creation of
ModelPoisReg- Attributes
features : {
numpy.ndarray,scipy.sparse.csr_matrix}, shape=(n_samples, n_features)The features matrix, either dense or sparse
labels :
numpy.ndarray, shape=(n_samples,) (read-only)The labels vector
n_samples :
int(read-only)Number of samples
n_features :
int(read-only)Number of features
n_coeffs :
int(read-only)Total number of coefficients of the model
n_threads :
int, default=1 (read-only)Number of threads used for parallel computation.
if
int <= 0: the number of threads available on the CPUotherwise the desired number of threads
dtype :
{'float64', 'float32'}, default=’float64’Type of the data arrays used.
Notes
The gradient and loss for the exponential link case cannot be overflow proof. In this case, only a solver working in the dual (such as
SDCA) should be used.In summary, use grad and call at your own risk when
link="exponential"-
__init__(fit_intercept: bool = True, link: str = 'exponential', n_threads: int = 1)[source]¶ Initialize self. See help(type(self)) for accurate signature.
-
dual_loss(dual_coeffs)[source]¶ Computes the dual loss at the given dual coefficients
- Parameters
dual_coeffs :
np.ndarrayDual coefficients
- Returns
dual_loss :
floatThe value of the dual loss
-
fit(features, labels)[source]¶ Set the data into the model object
- Parameters
features : {
numpy.ndarray,scipy.sparse.csr_matrix}, shape=(n_samples, n_features)The features matrix, either dense or sparse
labels :
numpy.ndarray, shape=(n_samples,)The labels vector
- Returns
output :
ModelPoisRegThe current instance with given data
-
grad(coeffs: numpy.ndarray, out: numpy.ndarray = None) → numpy.ndarray¶ Computes the gradient of the model at
coeffs- Parameters
coeffs :
numpy.ndarrayVector where gradient is computed
out :
numpy.ndarrayorNoneIf
Nonea new vector containing the gradient is returned, otherwise, the result is saved inoutand returned- Returns
output :
numpy.ndarrayThe gradient of the model at
coeffs
Notes
The
fitmethod must be called to give data to the model, before usinggrad. An error is raised otherwise.
-
hessian_norm(coeffs: numpy.ndarray, point: numpy.ndarray) → float¶ Computes the norm given by coeffs^top * H * coeffs here H is the hessian of the model computed at
point- Parameters
coeffs :
numpy.ndarrayVector where the hessian norm is computed
point :
numpy.ndarrayVector where we compute the hessian of the model
- Returns
output :
floatValue of the hessian norm
-
loss(coeffs: numpy.ndarray) → float¶ Computes the value of the goodness-of-fit at
coeffs- Parameters
coeffs :
numpy.ndarrayThe loss is computed at this point
- Returns
output :
floatThe value of the loss
Notes
The
fitmethod must be called to give data to the model, before usingloss. An error is raised otherwise.
-
loss_and_grad(coeffs: numpy.ndarray, out: numpy.ndarray = None) → tuple¶ Computes the value and the gradient of the function at
coeffs- Parameters
coeffs :
numpy.ndarrayVector where the loss and gradient are computed
out :
numpy.ndarrayorNoneIf
Nonea new vector containing the gradient is returned, otherwise, the result is saved inoutand returned- Returns
loss :
floatThe value of the loss
grad :
numpy.ndarrayThe gradient of the model at
coeffs
Notes
The
fitmethod must be called to give data to the model, before usingloss_and_grad. An error is raised otherwise.