Fit sparse and low rank adjacency matrix with Hawkes ADM4¶
Hawkes ADM4 algorithm (tick.inference.HawkesADM4) enforce sparse and low
rank adjacency matrix. It assumes hawkes model has been generated with
exponential kernels.
This algorithm has been introduced in the following paper:
Zhou, K., Zha, H., & Song, L. (2013, May). Learning Social Infectivity in Sparse Low-rank Networks Using Multi-dimensional Hawkes Processes. In AISTATS (Vol. 31, pp. 641-649).
Python source code: plot_hawkes_adm4.py
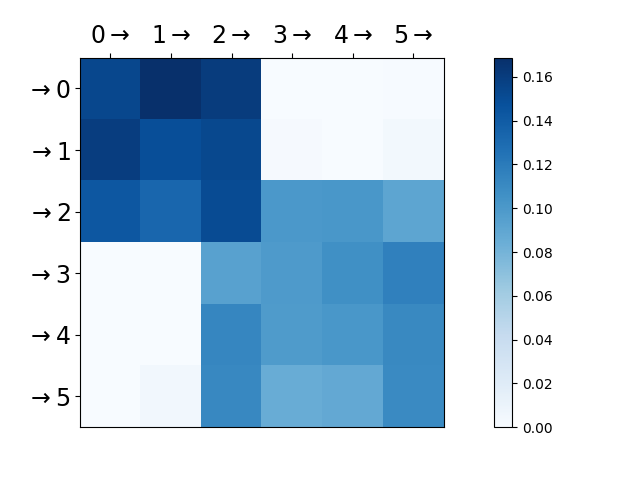
import numpy as np
from tick.plot import plot_hawkes_kernel_norms
from tick.hawkes import HawkesADM4, SimuHawkesExpKernels, SimuHawkesMulti
end_time = 10000
n_realizations = 5
decay = 3.
baseline = np.ones(6) * .03
adjacency = np.zeros((6, 6))
adjacency[2:, 2:] = np.ones((4, 4)) * 0.1
adjacency[:3, :3] = np.ones((3, 3)) * 0.15
hawkes_exp_kernels = SimuHawkesExpKernels(adjacency=adjacency, decays=decay,
baseline=baseline, end_time=end_time,
verbose=False, seed=1039)
multi = SimuHawkesMulti(hawkes_exp_kernels, n_simulations=n_realizations)
multi.end_time = [(i + 1) / n_realizations * end_time
for i in range(n_realizations)]
multi.simulate()
learner = HawkesADM4(decay)
learner.fit(multi.timestamps)
plot_hawkes_kernel_norms(learner)
Total running time of the example: 0.27 seconds ( 0 minutes 0.27 seconds)