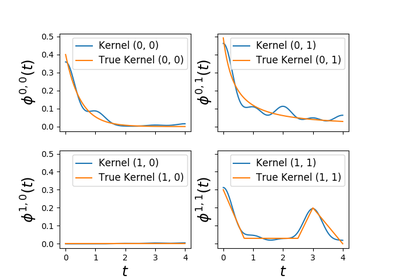
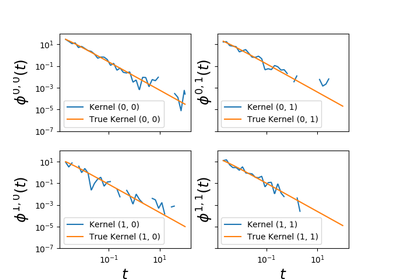
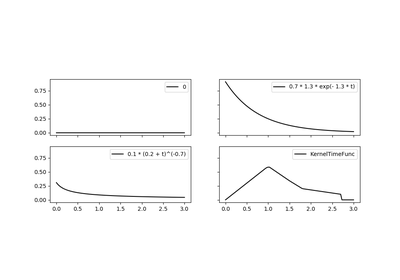
tick.hawkes.HawkesKernelPowerLaw¶
-
class
tick.hawkes.HawkesKernelPowerLaw(multiplier, cutoff, exponent, support=-1, error=1e-05)[source]¶ Hawkes kernel for power law
\[\phi(t) = \phi(t) = \alpha (\delta + t)^{- \beta} 1_{t > 0}\]Where \(\alpha\) is called the multiplier,
deltathe cut-off and \(\beta\) the exponent- Parameters
multiplier :
floatMultiplier of the kernel, also noted \(\alpha\)
cutoff :
floatCut-off of the kernel, also noted \(\delta\)
exponent :
floatExponent of the kernel, also noted \(\beta\)
-
__init__(multiplier, cutoff, exponent, support=-1, error=1e-05)[source]¶ Initialize self. See help(type(self)) for accurate signature.
-
get_norm(n_steps=10000)¶ Computes L1 norm
- Parameters
n_steps :
intnumber of steps used for integral discretization
Notes
By default it approximates Riemann sum with step-wise function. It might be overloaded if L1 norm closed formula exists
-
get_plot_support()¶ Returns support used to plot the kernel
-
get_support()¶ Returns the upperbound of the support
-
get_value(t)¶ Returns the value of the kernel at t
-
get_values(t_values)¶ Returns the value of the kernel for all times in t_values
-
is_zero()¶ Returns if this kernel is equal to 0