Asynchronous stochastic solver¶
This example illustrates the convergence speed of the asynchronous version of SVRG and SAGA solvers. This solver respectively called KroMagnon and ASAGA have been introduced in
Mania, H., Pan, X., Papailiopoulos, D., Recht, B., Ramchandran, K. and Jordan, M.I., 2015. Perturbed iterate analysis for asynchronous stochastic optimization. arXiv preprint arXiv:1507.06970..
R. Leblond, F. Pedregosa, and S. Lacoste-Julien: Asaga: Asynchronous Parallel Saga, (AISTATS) 2017.
To obtain good speedup in a relative short time example we have designed very sparse and ill-conditonned problem.
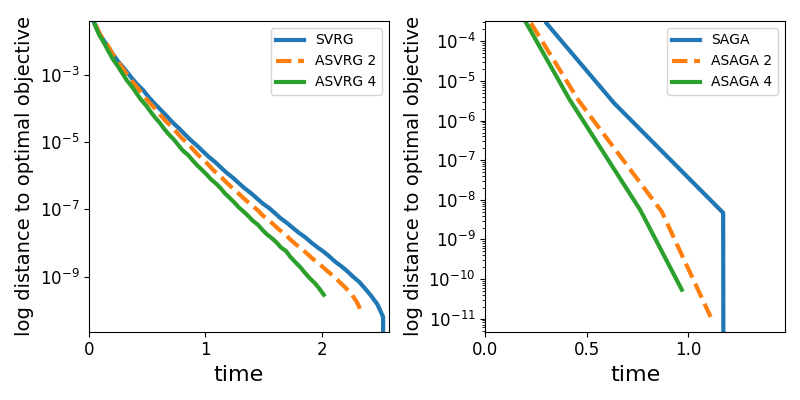
Python source code: plot_asynchronous_stochastic_solver.py
from scipy import sparse
import matplotlib.pyplot as plt
from tick.plot import plot_history
import numpy as np
from tick.linear_model import SimuLogReg, ModelLogReg
from tick.simulation import weights_sparse_gauss
from tick.solver import SVRG, SAGA
from tick.prox import ProxElasticNet
seed = 1398
np.random.seed(seed)
n_samples = 40000
n_features = 20000
sparsity = 1e-4
penalty_strength = 1e-5
weights = weights_sparse_gauss(n_features, nnz=1000)
intercept = 0.2
features = sparse.rand(n_samples, n_features, density=sparsity, format='csr')
simulator = SimuLogReg(weights, n_samples=n_samples, features=features,
verbose=False, intercept=intercept)
features, labels = simulator.simulate()
model = ModelLogReg(fit_intercept=True)
model.fit(features, labels)
prox = ProxElasticNet(penalty_strength, ratio=0.5, range=(0, n_features))
svrg_step = 1. / model.get_lip_max()
test_n_threads = [1, 2, 4]
fig, axes = plt.subplots(1, 2, figsize=(8, 4))
for ax, SolverClass in zip(axes, [SVRG, SAGA]):
solver_list = []
solver_labels = []
for n_threads in test_n_threads:
solver = SolverClass(step=svrg_step, seed=seed, max_iter=50,
verbose=False, n_threads=n_threads, tol=1e-10,
record_every=3)
solver.set_model(model).set_prox(prox)
solver.solve()
solver_list += [solver]
if n_threads == 1:
solver_labels += [solver.name]
else:
solver_labels += ['A{} {}'.format(solver.name, n_threads)]
plot_history(solver_list, x="time", dist_min=True, log_scale=True,
labels=solver_labels, ax=ax)
ax.set_ylabel('log distance to optimal objective', fontsize=14)
fig.tight_layout()
plt.show()
Total running time of the example: 43.76 seconds ( 0 minutes 43.76 seconds)