Fit exotic Hawkes kernels¶
This learner assumes Hawkes kernels are linear combinations of a given number of kernel basis.
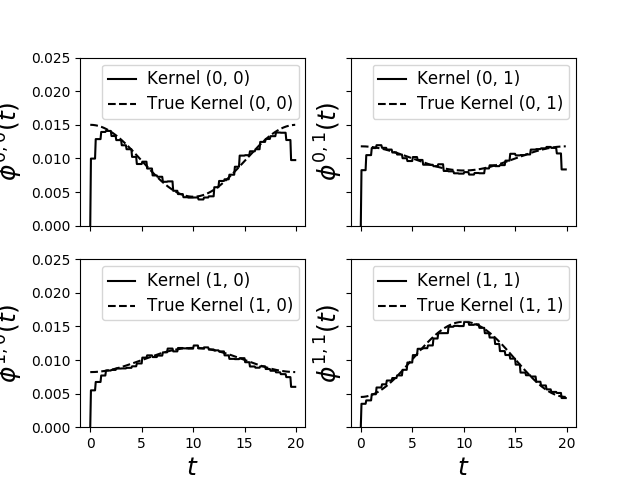
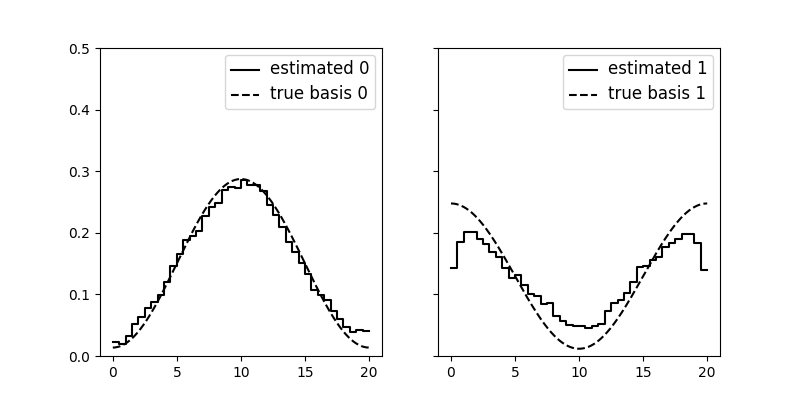
Here it is run on a an exotic data set generated with mixtures of two cosinus functions. We observe that we can correctly retrieve the kernels and the two cosinus basis functions which have generated the kernels. This experiment is run on toy datasets in the original paper.
It could have been more precise if end_time or kernel_size was increased.
Python source code: plot_hawkes_basis_kernels.py
import itertools
import numpy as np
import matplotlib.pyplot as plt
from tick.plot import plot_basis_kernels, plot_hawkes_kernels
from tick.hawkes import SimuHawkes, HawkesKernelTimeFunc, HawkesBasisKernels
end_time = 1e9
C = 1e-3
kernel_size = 40
max_iter = 100
# We first simulate a similar Hawkes process
def g1(t):
return np.cos(np.pi * t / 10) + 1.1
def g2(t):
return np.cos(np.pi * (t / 10 + 1)) + 1.1
t_values = np.linspace(0, 20, 1000)
u_values = [(0.007061, 0.001711), (0.005445, 0.003645), (0.003645, 0.005445),
(0.001790, 0.007390)]
hawkes = SimuHawkes(baseline=[1e-5, 1e-5], seed=1093, verbose=False)
for i, j in itertools.product(range(2), repeat=2):
u1, u2 = u_values[2 * i + j]
y_values = g1(t_values) * u1 + g2(t_values) * u2
kernel = HawkesKernelTimeFunc(t_values=t_values, y_values=y_values)
hawkes.set_kernel(i, j, kernel)
hawkes.end_time = end_time
hawkes.simulate()
ticks = hawkes.timestamps
# And then perform estimation with two basis kernels
kernel_support = 20
n_basis = 2
em = HawkesBasisKernels(kernel_support, n_basis=n_basis,
kernel_size=kernel_size, C=C, n_threads=4,
max_iter=max_iter, verbose=False, ode_tol=1e-5)
em.fit(ticks)
fig = plot_hawkes_kernels(em, hawkes=hawkes, support=19.9, show=False)
for ax in fig.axes:
ax.set_ylim([0, 0.025])
fig = plot_basis_kernels(em, basis_kernels=[g2, g1], show=False)
for ax in fig.axes:
ax.set_ylim([0, 0.5])
plt.show()
Total running time of the example: 1.26 seconds ( 0 minutes 1.26 seconds)