tick.base.TimeFunction

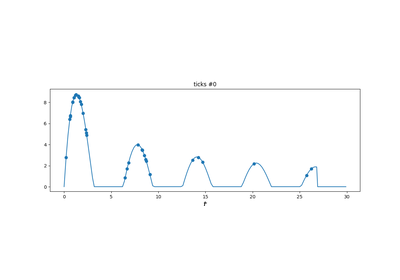
class tick.base.TimeFunction(values, border_type: int = 0, inter_mode: int = 0, dt: float = 0, border_value: float = 0)[source]

A function depending on time.

It is causal as its value is zero for all \(t < 0\).

Parameters

values : float or tuple

  • if a float is given the TimeFunction is constant and equal to this float

  • a tuple of two numpy arrays (t_values, y_values) where y is the value taken by the TimeFunction at times t

border_type : {Border0, BorderConstant, BorderContinue}, default=Border0

Handle the values returned after the after the last given t. This is only used if the TimeFunction is not a constant.

  • Border0 : value will be \(0\)

  • BorderConstant : value will be given by border_value

  • BorderContinue : value will equal to the last known value

  • Cyclic : value will be equal the value it would have had in the original given values, modulo the support.

inter_mode : {InterLinear, InterConstLeft, InterConstRight}, default=InterLinear

Handle the way we extrapolate between two known values. This is only used if the TimeFunction is not a constant.

  • InterLinear : value will be linearly interpolated following the formula \(f(x) = \frac{y_{t+1} - y_{t}}{x_{t+1} - x_{t}}\)

  • InterConstLeft : value will be equal to the next known point

  • InterConstRight : value will be equal to the previous known point

dt : float, default=0

The value used for the sub-sampling. If left to 0, it will be assigned automatically to a fifth of the smallest distance between two points

border_value : float, default=0

See border_type, BorderConstant case

Notes

TimeFunction are made to be very efficient when call if to get a specific value (\(\mathcal{O}(1)\)), however this leads us to have it taking a lot of space in memory.

Examples

>>> import numpy as np
>>> from tick.base import TimeFunction
>>> t_values = np.array([0, 1, 2, 5], dtype=float)
>>> y_values = np.array([2, 4.1, 1, 2], dtype=float)
>>> linear_timefunction = TimeFunction([t_values, y_values])
>>> # By default the time function will give a linear interpolation from 
>>> # the two nearest points for any time value
>>> '%.2f' % linear_timefunction.value(2)
'1.00'
>>> '%.2f' % linear_timefunction.value(3)
'1.33'
>>> # and it equals 0 outside of its bounds
>>> linear_timefunction.value(-1)
0.0
>>> linear_timefunction.value(7)
0.0
__init__(values, border_type: int = 0, inter_mode: int = 0, dt: float = 0, border_value: float = 0)[source]

Initialize self. See help(type(self)) for accurate signature.

get_norm()[source]

Computes the integral value of the TimeFunction

value(t)[source]

Gives the value of the TimeFunction at provided time

Parameters

t : float or np.ndarray

Time at which the value is computed

Returns

output : float or np.ndarray

TimeFunction value at provided time